Waar hebben we het in vredesnaam over, Évariste Galois?

Voordat we in het cryptografische konijnenhol duiken, laten we eens kijken wat Galois-velden eigenlijk zijn. Genoemd naar de jonge Franse wiskundige Évariste Galois (die, leuk weetje, op 20-jarige leeftijd in een duel stierf - een spectaculaire manier om te gaan), zijn deze velden eindige verzamelingen van elementen met speciale algebraïsche eigenschappen.

In eenvoudigere termen, stel je een speelplaats voor waar getallen zich aan heel specifieke regels houden. Deze regels zorgen ervoor dat, hoe je deze getallen ook optelt, aftrekt, vermenigvuldigt of deelt (behalve door nul, want zelfs in de wiskunde kunnen we niet door nul delen), je altijd weer een getal in dezelfde speelplaats krijgt.

De Crypto-Connectie: Waarom Galois-velden Belangrijk Zijn

Nu denk je misschien, "Leuk verhaal, maar wat heeft dit te maken met het veilig houden van mijn kattenmemes?" Goede vraag! Galois-velden vormen de ruggengraat van verschillende minder bekende, maar steeds belangrijker wordende cryptografische systemen. Hier is waarom ze zoveel ophef veroorzaken:

  • Efficiëntie: Operaties in Galois-velden kunnen ongelooflijk snel en efficiënt zijn, wat cruciaal is voor real-time encryptie.
  • Weerstand: Ze bieden sterke weerstand tegen bepaalde soorten cryptografische aanvallen.
  • Flexibiliteit: Galois-velden van verschillende groottes kunnen worden gebruikt om verschillende niveaus van beveiliging te creëren, waardoor ze aanpasbaar zijn aan verschillende behoeften.

Galois-velden in Actie: Cryptografische Systemen in de Praktijk

Laten we eens kijken naar enkele cryptografische systemen die Galois-velden gebruiken:

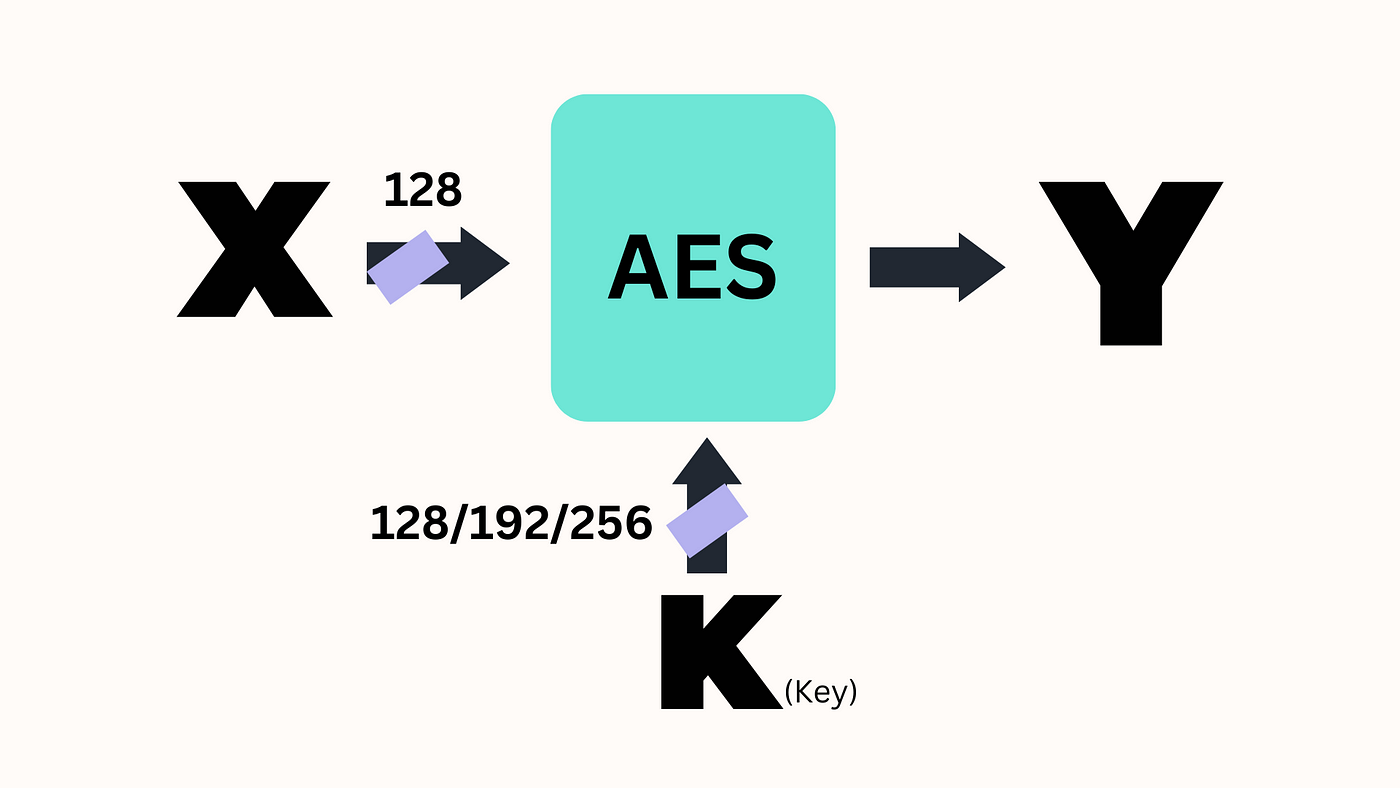
1. Advanced Encryption Standard (AES)

Ja, die AES. Hoewel het niet precies "next-gen" is, gebruikt AES operaties in het Galois-veld GF(2^8) voor zijn MixColumns-stap. Dit helpt bij het creëren van de verwarring en diffusie die nodig zijn voor veilige encryptie.

2. Reed-Solomon Foutcorrectie

Hoewel het voornamelijk wordt gebruikt voor foutcorrectie bij datatransmissie en -opslag, hebben Reed-Solomon-codes, gebaseerd op Galois-veldrekenkunde, ook toepassingen in cryptografie, met name in geheime deelregelingen.

3. Elliptische Curve Cryptografie (ECC)

ECC werkt over eindige velden, vaak Galois-velden. Dit maakt kleinere sleutelmaten mogelijk in vergelijking met RSA, terwijl gelijkwaardige beveiligingsniveaus behouden blijven.

De Volgende Grens: Post-Quantum Cryptografie

Hier wordt het echt interessant. Nu quantumcomputers aan de horizon verschijnen en dreigen veel van onze huidige encryptiemethoden te breken, wenden cryptografen zich tot Galois-velden om quantum-resistente algoritmen te ontwikkelen.

Code-gebaseerde Cryptografie

Een veelbelovend gebied is code-gebaseerde cryptografie, die sterk afhankelijk is van operaties in Galois-velden. Het McEliece-cryptosysteem, bijvoorbeeld, gebruikt foutcorrigerende codes over eindige velden om een openbaar-sleutel encryptiesysteem te creëren dat als quantum-resistent wordt beschouwd.

Hier is een vereenvoudigd voorbeeld van hoe een Galois-veld kan worden gebruikt in code-gebaseerde cryptografie:


import galois

# Maak een Galois-veld van grootte 2^8
GF = galois.GF(2**8)

# Genereer een willekeurig bericht
message = GF.Random(10)

# Genereer een willekeurige foutvector
error = GF.Random(10)

# Simuleer codering en voeg fout toe
encoded_message = message + error

# In werkelijkheid zou decodering complexe algoritmen omvatten
# met behulp van eigenschappen van het Galois-veld
decoded_message = encoded_message - error

print(f"Origineel bericht: {message}")
print(f"Gedecodeerd bericht:  {decoded_message}")
print(f"Zijn ze gelijk?   {all(message == decoded_message)}")

Dit is natuurlijk een zeer vereenvoudigd voorbeeld. Echte code-gebaseerde cryptosystemen omvatten veel complexere operaties en grotere veldgroottes.

Uitdagingen en Overwegingen

Voordat je al je cryptocode herschrijft met Galois-velden, laten we enkele uitdagingen overwegen:

  • Complexiteit: Werken met Galois-velden vereist een goed begrip van abstracte algebra. Het is niet voor de zwakkeren (of wiskundigen).
  • Implementatie: Efficiënte implementatie van Galois-veldrekenkunde kan lastig zijn, vooral op hardware die niet is geoptimaliseerd voor deze operaties.
  • Standaardisatie: Veel op Galois-veld gebaseerde cryptosystemen bevinden zich nog in de onderzoeksfase en zijn nog niet breed gestandaardiseerd.

Dus, Wat is het Grote Probleem?

Galois-velden zijn meer dan alleen een wiskundige curiositeit. Ze vormen de basis voor een nieuwe generatie cryptografische systemen die sneller, efficiënter en mogelijk quantum-resistent beloven te zijn. Terwijl we een tijdperk ingaan waarin databeveiliging belangrijker is dan ooit, zullen deze wiskundige structuren waarschijnlijk een steeds belangrijkere rol spelen in het veilig houden van ons digitale leven.

Of je nu een cryptografie-enthousiasteling bent, een beveiligingsprofessional, of gewoon iemand die slim wil klinken op feestjes, het begrijpen van de rol van Galois-velden in moderne cryptografie is zeker de moeite waard. Wie weet? De volgende doorbraak in databeveiliging zou zomaar uit deze eindige velden van oneindige mogelijkheden kunnen komen.

"De kunst van het doen van wiskunde bestaat erin dat speciale geval te vinden dat alle kiemen van algemeenheid bevat." - David Hilbert

En in het geval van moderne cryptografie zou dat speciale geval wel eens Galois-velden kunnen zijn. Dus de volgende keer dat iemand je vraagt naar de toekomst van encryptie, kun je vol vertrouwen zeggen: "Het draait allemaal om die Galois, 'bout die Galois, geen probleem."

Verder Lezen

Als je nieuwsgierig bent en dieper wilt duiken in de wereld van Galois-velden en hun toepassingen in cryptografie, hier zijn enkele bronnen om je op weg te helpen:

Onthoud, in de wereld van cryptografie is de cutting-edge van vandaag de verouderde van morgen. Blijf nieuwsgierig, blijf leren, en wie weet? Misschien ben jij wel degene die de volgende grote doorbraak in crypto ontdekt. Moge de Galois met je zijn!